How much thought have you put into the nature of randomness in your game? May I suggest taking a moment and considering it, its nature, and how it could go wrong?
There are some people who don’t think games should be random, or that die rolls at least should play a minimal role. Put all the information out there for the player. If an attack works, it should be definite; get the uncertainty out of it. In an action game, if you point at a player with a gun and pull the trigger, if your aim was true, the target should be hit. No random drift or aiming stat should interfere.
Then there are some who, so concerned are they about people’s misconceptions about what it means to say an attack is 90 percent likely to hit, actually fudge the math, and roll the dice so that it actually means the attack is more like 98 percent likely to hit.
There are few computer games that use what we would call true randomness. In our macro-scaled, Newtonian world, randomness is actually rare. When we roll dice, the outcome is determined largely when the solids leave our hand. What we substitute for randomness is, in actuality, ignorance. We don’t know the consequences of the motion vectors of the dice as they sail through the air, nor how they’ll react when they strike the table, how they’ll tumble and come to rest. Good enough for Monopoly.
You can access true randomness at quantum scales, but this is generally out of reach through conventional electronics. The issue is of enough importance that some Unix-based systems actually maintain a pool of “entropy,” gathered through sources such as the precise timing of user inputs, as an OS-level service, making it available to programs on request. These requests are important enough that they can be set to block, pausing the requesting process, until enough entropy is generated (like through pressing keys or moving the mouse around) to satisfy them. Those are usually intended for cryptographic use.
"You can access true randomness at quantum scales, but this is generally out of reach through conventional electronics."
Less important requests are usually made up for through other methods. Most of the time, what we have to work with in entertainment software are pseudo-random number generators, which are well-understood, supplied with most compilers through standard libraries, and if need be, can be implemented yourself.
And yet, particularly enthusiastic users, especially in the speedrunning community, have drawn attention to these lowly workhorses. They're well worth studying if you're a game maker thinking about how (or if) to implement RNG in your own game; with that in mind, here are three notably different game RNGs, their natures, how they’re used, and in a couple of cases how they’ve been exploited.
Final Fantasy I: Reading sequentially from a list of pre-generated numbers
The original Final Fantasy, and a few other early Square Famicom games, were programmed by Nasir Gebelli, a legendary 8-bit programmer who made a name for himself on the Apple II. The Apple II and Famicom are both 6502-based machines, so Gebelli came to the system with an assortment of tricks under his belt.
One of them is that its encounter random generation is mostly handled by walking up or down through a preset table of 256 values stored in ROM. The index is updated every step (going up or down according to a convoluted process), and the value pointed to compared to a threshold value. If the value is beneath the threshold, an encounter is generated.
Essentially this system is a list of randomish numbers that get reused again and again. The index, notably, is reset when the system is reset.

This is not the original Final Fantasy’s only RNG. During battles, when a die roll is needed, a similar system is used, with a completely different table of 256 randomish values, although this one is read sequentially. Unlike the encounter generator’s index, this one is saved in the battery-backed RAM, meaning, among other things, if you have an encounter after loading a save in a given area, reload the game, then have an encounter in the same area, it will be the same group of enemies, with the same surprise determination.
Interestingly, while the state of the battle random generator (its seed) is saved on the battery-backed RAM, it is not tied to any player’s save file.
After a battle begins, the battle engine does a fairly smart thing. Every two frames, the game calls the random number function but doesn’t use the result, advancing the table to a difficult-to-predict place.
We could call this kind of act, generating numbers not for their values but just to advance the generator, “spinning” the RNG. When the player moves the cursor, the RNG is spun an additional time. The result ties the outcome of battle calculations to the timing of the player’s actions in a way that’s difficult to duplicate between plays. Although the encounter group and surprise status may be the same every time after loading a save, unless the player can duplicate his actions within a 30th of a second accuracy, the states will soon diverge.
That word, diverge, is important. Without outside access to allow it to behave otherwise, a computer program in one state will, provided proper operation, without fail progress along the same track. In an RPG, care must be taken so that a player cannot game the random number generator to create advantageous states. If you know ahead of time, for instance, that being in a given area will result an unwanted encounter, you could arrange, just for that step, to be in a different encounter zone. You could even use this to shop around, and find the encounter zone that produces the best opponents for your fight.
"On the Commodore 64, the output of the noise oscillator on the sound chip, while not perfect, was often used as a good-enough source of entropy."
The only way to get out of this, to diverge from this state, is to obtain some outside value, some external source of entropy, that the program can use to vary its running state. On the Commodore 64, the output of the noise oscillator on the sound chip, while not perfect, was often used as a good-enough source of entropy. Sometimes on the NES and SNES, a game will spin the RNG on some or all frames. Since the reactions to the player’s inputs would occur on different frames, over time this would cause the operation of the program to diverge more and more as the player’s behavior provides entropy to the system.
Systems with a real-time clock will often use a hash of that to initialize pseudo-random generators, although since usually the clock is settable by the player, that can also become a possible exploit. It’s most useful if the clock has a fine resolution, we’re talking milliseconds, since by taking the low digits of its value you can end up with a value that’s very hard for the player to usefully manipulate.
Back to Final Fantasy. This is all, for the most part, too fiddly to be taken advantage of by casual players, even if they could do the work to figure out the state of the random seed. But what if there is a particularly difficult encounter that a player might want to avoid, or perhaps trigger, for some reason?
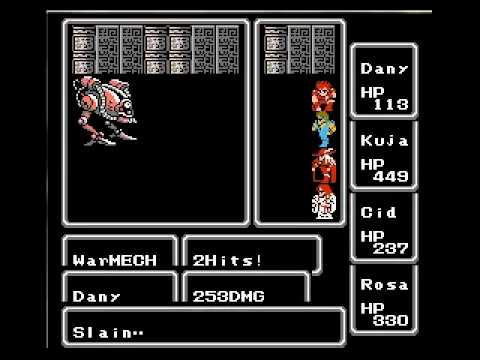
In one room of the game, there is a legendary pseudoboss called Warmech. It appears in a room with a very high enemy encounter rate, but it is a member of enemy encounter group 8. The table the game reads from when determining random monsters does so by reading the low bits of a value, and the table is constructed so that only three values in the table will cause it to set up encounter group 8, meaning Warmech is generated only 3 times in 256 battles. If you know the state of the battle generator, you could engineer this encounter, forcing it to happen.
Speedrunners have analyzed all of this. At AGDQ 2017, runners Gyre and Feasel used these facts, and others, to keenly manipulate enemy generation, avoid high risk/low reward encounters, gain levels in an optimized way, and generally make a mockery of the idea of randomness. See it for yourself here.
Super Mario 64: Linear Congruential Generator
A popular source of pseudo-random numbers, provided that they don’t produce game-breaking effects if manipulated, is what’s called a linear congruential random number generator (LCRNG). It is worth looking that up on Wikipedia. The essence of a good LCRNG is a kind of counter that doesn’t count sequentially. Its value jumps around, yet it will still step through nearly all of its domain.

Basically you start with a seed value. You perform some basic arithmetic operations on it to get a result value, which is both returned to the caller and used to reseed the generator. You end up with a sequence of values that progresses forward from each possible seed. If you ever were to end up with a seed that, at some point, produces itself after some number of runs, you’d end up with a cycle. The result values would reoccur at the point where the seed reproduced itself. An RNG algorithm has to avoid these kinds of situations where possible. This is a reason that LCRNGs can make good RNGs: chosen well, they won’t cycle until they nearly exhaust their domain, and they’re quick both to implement and run using basic math.

Such a LFSR is used in Super Mario 64. Mario 64
No tags.