Objective
The main objective of this blog post is to give you a basic idea about how to work with Bezier Curve In Games.
Step 1 Introduction
Bezier curves are the most fundamental curves, used generally in computer graphics and image processing. Bezier curves can be used for creating smooth curved roads, curved paths just like zuma game, curved shaped rivers, etc. in your game.
A Bezier curve is defined by a set of control points P0 through Pn, where n is called its order (n = 1 for linear, 2 for quadratic, etc.). The first and last control points are always the end points of the curve; however, the intermediate control points (if any) generally do not lie on the curve.
Bezier curve containing two control points i.e. n = 2 is called a Linear Bezier Curve
Bezier curve containing three control points i.e. n = 3 is called a Quadratic Bezier Curve
Bezier curve containing four control points i.e. n = 4 is called a Cubic Bezier Curve and so on.
Bezier function, that returns points on bezier curve uses concept of linear interpolation as base. So, Let’s understand what is Linear Interpolation first.
Step 2 Linear Intrepolation
Linear interpolation between two points means getting interpolated point for different values of t between those two points, where 0 < t < 1, just like Mathf.Lerp.
Formula for interpolated point, P between P0 and P1 can be written as,
P = P0 + t(P1 – P0) , 0 < t < 1
Here, for getting interpolated point we are adding tth fraction of distance between those two points to P0. So,
For t=0,P = P0.
For t=1, P = P1.
For t=0.5, P = Intermediate point between P0 and P1.
Step 3 Linear Bezier Curves
Linear Bezier curve has two control points. For given two points P0 and P1, a Linear Bezier curve is simply a straight line between those two points. The curve is equivalent to linear interpolation and is given by,
B(t) = P0 + t(P1 – P0) = (1-t) P0 + tP1 , 0 < t < 1
Animation of how a linear bezier curve is calculated is shown below:
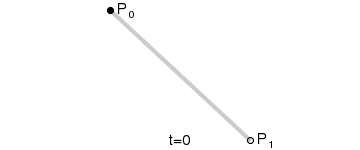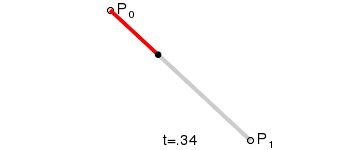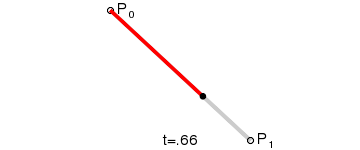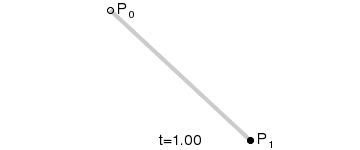
bezier_linear
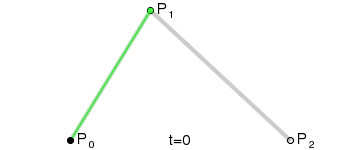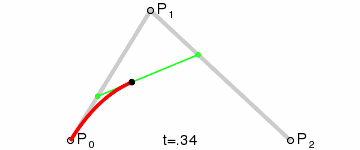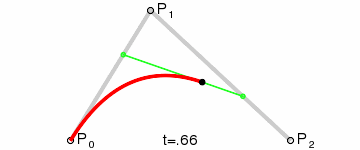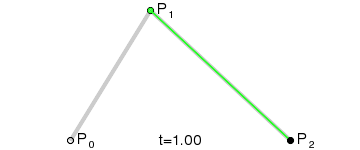
Step 4 Quadratic Bezier Curves
Quadratic bezier curve has three control points. Quadratic Bezier curve is a point-to-point linear interpolation of two Linear Bezier Curves. For given three points P0, P1 and P2, a quadratic bezier curve is a linear interpolation of two points, got from Linear Bezier curve of P0 and P1 and Linear Bezier Curve of P1 and P2. So, Quadratic bezier curve is given by,
B(t) = (1-t) BP0,P1(t) + t BP1,P2(t), 0 < t < 1
B(t) = (1-t) [(1-t) P0 + tP1] + t [(1-t) P1 + tP2] , 0 < t < 1
By rearranging the above equation,
B(t) = (1-t)2P0 + 2(1-t)tP1 + t2P2 , 0 < t < 1
Animation of how quadratic bezier curve is calculated is shown below:
bezier_quadratic
Step 5 Cubic Bezier Curves
Cubic Bezier curve has four control points. Quadratic bezier curve is a point-to-point linear interpolation of two Quadratic Bezier curves. For given four points P0, P1, P2 and P3





































