The physics of trains in Assassin's Creed Syndicate

In this article, I would like to present our custom simulator which we created to model the physics of trains in Assassin's Creed Syndicate. The game is set in the year 1868 in London during the times of the industrial revolution when steam and steel marked the progress of the society. It was a great pleasure to work on this unique opportunity of bringing to life the world of Victorian Era London. Attention to the historical and the real-world details led us to the creation of this physically-based simulation.

Introduction

It is not common these days to write your own physics engine. However, there are situations when it is very useful to create your own physical simulator from the ground up. Such situations might occur when there are specific conditions or needs for a new gameplay feature or a part of the simulated game world. This is the situation which we came across when developing railway system and the whole management of trains running in the 19^th-century London.

The standard coupling system for trains in Europe is presented in figure 1 on the left. The same system was used in 19^th-century trains in London [1]. When we started our work on trains we quickly realized that we can create interesting interactions and behaviors when physically simulating the chain. So instead of having rigidly connected wagons, we have them connected with the movable coupling chain which drives the movement for all wagons in the train.

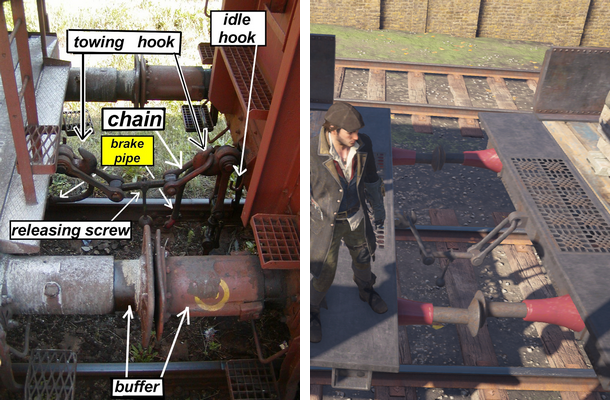
Figure 1. Chain coupler details on the left (source: Wikipedia [1]). The coupling system in Assassin’s Creed Syndicate on the right.

There are a couple of advantages for our own physics solution in this case:

Here is the video with our physics of trains in action:

<iframe title="The physics of trains in Assassin's Creed Syndicate - Video 1" src="//www.youtube.com/embed/w8hhUeNxo-w?rel=0&amp;enablejsapi=1&amp;origin=https%3A%2F%2Fwww.gamedeveloper.com" height="360px" width="100%" data-testid="iframe" loading="lazy" scrolling="auto" class="optanon-category-C0004 ot-vscat-C0004 " data-gtm-yt-inspected-91172384_163="true" id="745341499" data-gtm-yt-inspected-91172384_165="true" data-gtm-yt-inspected-113="true"></iframe>

We will start with the section explaining first how we control our trains.

Note:

To simplify our discussion, we use the word “tractor” to describe a wagon closer to the locomotive and the word “trailer” to describe a wagon closer to the end of the train.

Controlling locomotive

We have a very simple interface to control the locomotive – which consists of requesting a desired speed:

Locomotive::SetDesiredSpeed(float DesiredSpeed, float TimeToReachDesiredSpeed)

Railway system manager submits such requests for every train running in the game. To execute the request, we calculate a force needed to generate desired acceleration. We use the following formula (Newton’s second law):

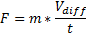
where F is computed force, m is the locomotive’s mass, 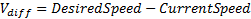, and t = TimeToReachDesiredSpeed.

Once the force is calculated, we send it to WagonPhysicsState as an “engine force” to drive the locomotive (more information about it in the next section).

Because the physical behavior of the train can depend for example on the number of wagons (wagons colliding with each other creating a chain reaction and pushing the train forward), we need a way to ensure that our desired speed request once submitted is fully executed. To achieve this, we re-evaluate the force needed to reach desired speed every 2 seconds. This way we are sure that the request once submitted is finally reached. But as a result, we are not able to always satisfy TimeToReachDesiredSpeed exactly. However, small deviations in time were acceptable in our game.

Also, to keep the speed of the locomotive as given by SetDesiredSpeed request, we do not allow the coupling chain constraint to change the speed of the locomotive. To compensate the lack of such constraint impulses, we created a special method to model the dragging force – more about it in the section “the start-up of the train”. Finally, we do not allow collision response to modify the speed of the locomotive except when the train decelerates to a zero speed.

In the next section, we describe our basic level of the physical simulation.

Basic simulation step

This is a structure used to keep physical information about every wagon (and locomotive):

struct WagonPhysicsState
{
    // Values advanced during integration: 
    // distance along the track and momentum.
    RailwayTrack m_Track;
    float m_LinearMomentum;

    // Speed is calculated from momentum.
    float m_LinearSpeed;

    // Current value of forces.
    float m_EngineForce;
    float m_FrictionForce;

    // World position and rotation obtained directly from the railway track.
    Vector m_WorldPosition;
    Quaternion m_WorldRotation;

    // Constant during the simulation:
    float m_Mass;
}

As we can see there is no angular velocity. Even if we check collisions between wagons using 3D boxes (with rotation always aligned to the railway line) trains are moving in the 1D world along the railway line. So there is no need to keep any information about the angular movement for the physics. Also, because of the 1D nature of our simulation, it is enough to use floats to store physical quantities (forces, momentum and speed).

For every wagon we use Euler method [2] as a basic simulation step (dt is the time for one simulation step):

void WagonPhysicsState::BasicSimulationStep(float dt)
{
    // Calculate derivatives.
    float dPosition = m_LinearSpeed;
    float dLinearMomentum = m_EngineForce + m_FrictionForce;

    // Update momentum.
    m_LinearMomentum += dLinearMomentum*dt;
    m_LinearSpeed = m_LinearMomentum / m_Mass;

    // Update position.
    float DistanceToTravelDuringThisStep = dPosition*dt;
    m_Track.MoveAlongSpline( DistanceToTravelDuringThisStep );

    // Obtain new position and rotation from the railway line.
    m_WorldPosition = m_Track.GetCurrentWorldPosition();
    m_WorldRotation = m_Track.AlignToSpline();
}

We use three main equations to implement our BasicSimulationStep. These equations state that velocity is a derivative of position and force is a derivative of momentum (dot above the symbol indicate derivative with respect to time) [2 - 4]:

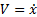
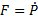
The third equation defines momentum P, which is a multiplication of mass and velocity:

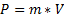
In our implementation, applying an impulse to the wagon is just an addition operation to the current momentum:

void WagonPhysicsState::ApplyImpulse(float AmountOfImpulse)
{
    m_LinearMomentum += AmountOfImpulse;
    m_LinearSpeed = m_LinearMomentum / m_Mass;
}

As we can see, immediately after changing momentum we are recalculating our speed for an easier access to this value. This is done in the same way as in [2].

Now, when we have the basic method to advance the time in our simulation, we can move forward to the other parts of our algorithm.

High-level steps of the simulation for one train

Here is the pseudo code for the full simulation step for one train:

// Part A
Update train start-up velocities

// Part B
For all wagons in train
    ApplyDeferredImpulses

// Part C
For all wagons in train
    UpdateCouplingChainConstraint

// Part D
For all wagons in train
    UpdateEngineAndFrictionForces
    SimulationStepWithFindCollision
    CollisionResponse

It is important to mention that, as it is written in the pseudo-code, every part is executed consecutively for all wagons in one train. Part A implements specific behavior related to the start-up of the train. Part B applies deferred impulses that come from collisions. Part C is our coupling chain solver – to be sure that we do not exceed maximum distance for the chain. Part D is responsible for engine and friction forces, the basic simulation step (integration) and handling collisions.

In our simulation algorithm, we always keep the same order of updates for wagons in the train. We start from the locomotive and proceed consecutively along every wagon from the first one to the last one in the train. Because we are able to use this specific property in our simulator, it makes our calculations easier to formulate. We use this characteristic especially for collision contact – to consecutively simulate every wagon’s movement and check collisions only with one other wagon.

Every part of this high-level simulation loop is explained in details in the following sections. However, because of its importance, we start with part D and SimulationStepWithFindCollision.

Simulation with collisions

Here is the code for our function SimulationStepWithFindCollision:

WagonPhysicsState SimulationStepWithFindCollision(WagonPhysicsState InitialState, float dt)
{
    WagonPhysicsState NewState = InitialState;
    NewState.BasicSimulationStep( dt );
    bool IsCollision = IsCollisionWithWagonAheadOrBehind( NewState );
    if (!IsCollision)
    {
        return NewState;
    }
    return FindCollision(InitialState, dt);
}

First, we perform tentative simulation step using the full delta time by calling

NewState.BasicSimulationStep( dt );

and checking if in a new state we have any collisions:

bool IsCollision = IsCollisionWithWagonAheadOrBehind( NewState );

If this method returns false, we can use this newly computed state directly. But if we have a collision, we execute FindCollision to find a more precise time and physics state just before the collision event. To perform this task we are using binary search in a similar manner as in [2].

This is our loop to find the more precise time of collision and physics state:

WagonPhysicsState FindCollision(WagonPhysicsState CurrentPhysicsState, float TimeToSimulate)
{
    WagonPhysicsState Result = CurrentPhysicsState;

    float MinTime = 0.0f;
    float MaxTime = TimeToSimulate;
    for (int step = 0 ; step<MAX_STEPS ; ++step)
    {
        float TestedTime = (MinTime + MaxTime) * 0.5f;

        WagonPhysicsState TestedPhysicsState = CurrentPhysicsState;
        TestedPhysicsState.BasicSimulationStep(TestedTime);
        if (IsCollisionWithWagonAheadOrBehind(TestedPhysicsState))
        {
            MaxTime = TestedTime;
        }
        else
        {
            MinTime = TestedTime;
            Result = TestedPhysicsState;
        }
    }

    return Result;
}