Jacques Kerner is a senior software engineer at Avalanche Studios. In this article, he discusses the work put into Just Cause 3's boat physics.

Welcome to part 2 of the series on boat physics for video games. In part 1, I explained the principles of buoyancy and how we chose to calculate the hydrostatic forces acting on a boat. I also stated that we were laying an important foundation for calculating not only the hydrostatic forces but also the hydrodynamic forces of our simplified model. By this I meant that we will compute additional forces on each submerged triangle, sum them up, and apply them to the boat. It's that simple.

Or so one could think at first. It turned out that modeling the rest of the forces to give the boat an acceptable dynamic response took much more research and iteration than laying all the foundation presented in part 1 and computing the buoyancy. Retrospectively, in comparison, the first part was a walk in the park. That second part felt like running an obstacle course in a foggy jungle full of spear pits, while pursued by angry wolves (a.k.a. producers).

If you haven't read part 1, here's a quick summary. The boat is modeled as a triangulated mesh. We approximate the surface of the water with a height field, and, using a fast approximate triangle vs height field intersection algorithm, we determine the part of the boat lying below the water, as a list of fully submerged triangles. Each triangle of the original mesh can produce 0, 1, or 2 fully submerged triangles. You can see the algorithm at work in figure 1.

Figure 2 illustrates the typical hydrostatic pressure distribution over the submerged part of the boat. The coarse approximation is that we consider the pressure constant over a submerged triangle. The motion of the boat shown here is not the result of hydrostatic forces only.

Figure 2 - Hydrostatic pressure distribution obtained with our model. Note that this behavior was obtained with the full model, not by applying only hydrostatic forces to the boat. The boat is dropped from 2 meters high and given some time to settle. It is then teleported 2 meters under water and left to rise to the surface and settle again. The pressure is considered constant over an entire submerged triangle, which can be quite big. The bigger the hull triangles, the coarser the approximation. However the model works and is stable even with fairly low poly meshes. Good enough for army work!

As can be seen in figure 3, applying only the hydrostatic forces is not enough to accurately simulate a body in water. To me, this is what is great about programming and simulation. It gives us the ability to verify if a given model is close to describing a real physical phenomenon. While we are hopelessly slow at coming up with good models for physical phenomena, especially in accurate mathematical terms, our eyes and brain are astoundingly good and fast at detecting when a simulation doesn't capture their essence to a high order of precision. In this case, the simulation shows us how important resistive forces are for a boat, and what it would look like if these resistive forces didn't exist, in some kind of weird, very bouncy, parallel universe.

Figure 3 - Dynamic response of a boat subjected to hydrostatic forces only, on perfectly flat water. It would get pretty messy in there with a fishing line. It's clear that resistance forces play a big role in reality.

In figure 3, it looks like the boat is mounted on a spring rather than floating in water. We know from experience that a boat dropped from a height, would very quickly stop bouncing up and down. This is called damping, the attenuation of motion by forces opposing it. As a result, the maximum height reached by consecutive peaks in an up and down motion gets smaller and smaller. In the case of critical damping, the forces are strong enough to prevent oscillations altogether.

Fun with JC3's light patrol boat. The water simulation is provided by NVIDIA WaveWorks.

Stabilizing the model

When I set out to develop a simple model of the forces acting on the boat, I only had a nebulous plan of what I wanted to achieve. It could be summed up as a mix between "developing a stable boat model that reacts to big waves in a realistic manner and is fun to drive" and "seriously, how hard can it be". While we figured out the forces to apply to the boat, we needed to stabilize it so it wouldn't bounce uncontrollably. Also, if we introduced forces which were too big or unstable, we needed a safety net to prevent the boat from reaching insane speeds. So the first thing we did was to add some strong damping forces, both for the linear and angular components, to stabilize the oscillation I just mentioned. The damping is simply proportional to how much the floating body is submerged in water. As you may recall, at every frame, we determine a list of submerged triangles, so a simplistic measure of how much the boat is submerged is given by the ratio between the submerged area and the total surface area of the boat.

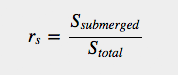
We can introduce a linear damping force looking like this for instance:

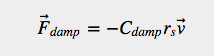
or a quadratic damping:

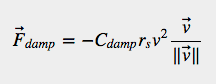
Before we dive in: a spoiler

In the end, we used 3 different forces coming from the interaction between the boat and water: viscous water resistance, pressure drag, and slamming force (or water entry force). Each of these forces was added to the model because they somewhat correspond to a reality, and also because they address a certain problem. In the rest of the article, I explain which physical reality each of these forces is meant to represent, and I also explain what motivated us to include the force, i.e. which specific set of problems the force addresses. Remember that this is a simplified model, so some of the forces are only vaguely related to a physical reality. This is especially the case of the pressure drag, which is a gross simplification of what is referred to as wave resistance and spray resistance, in more advanced hydrodynamic theory. A fourth force, the added mass force, didn't make it in the model in the end, but I still wonder how it could be factored in to give a better sense of inertia.

The drag equation

Since a lot of the discussion ahead of us is about drag, I want to pause for a second and look at the drag equation. If you are familiar with it you can skip ahead to the next section. In fluid dynamics, the tradition is to express drag in the form:

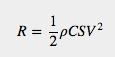
Ingredients of the triangle

Before I start describing our model of hydrodynamic forces, I introduce a few quantities and vectors related to the submerged triangles of the boat hull. All forces are computed using these.

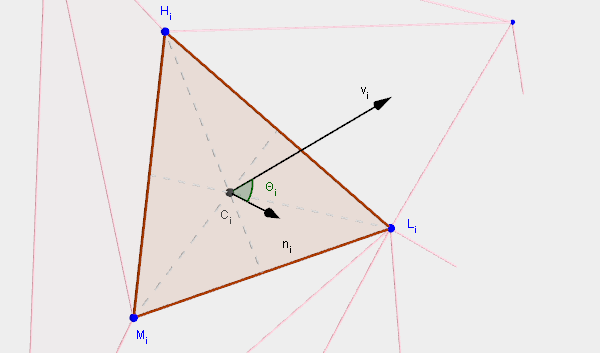
Figure 5 - Some useful quantities on each submerged triangle

Viscous Water Resistance

As in many texts on hydrodynamics, I will start with viscous water resistance. Viscous resistance occurs when water flows across a surface. Because there is strong interaction between the water immediately next to the hull and the surface of the hull, there is a microscopic layer of water that essentially "sticks" to the surface, and moves with the boat. Then as the distance increases away from the hull, the water sticks less and less. To simplify a little bit, each microscopic layer of water at a given distance from the surface interacts with - "sticks to" - the one immediately before it and the one immediately after. The intensity of that interaction is called viscosity. The more viscous a fluid, the more of it will stick to a surface and be dragged along with it. (*). This creates a force called viscous water resistance.

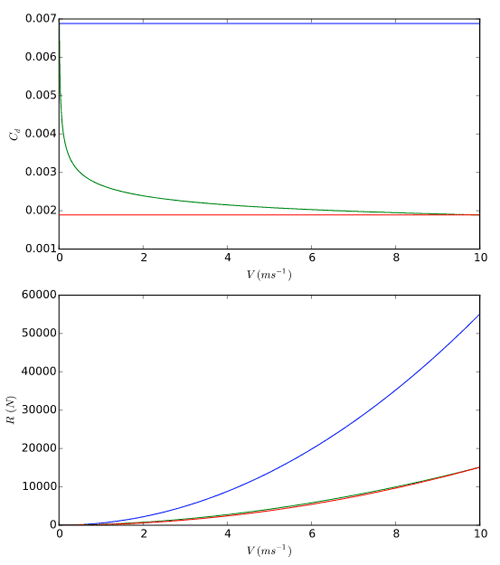
A lot of experiments have been conducted to measure viscous water resistance and there are good empirical formulas for predicting how much viscous water resistance a boat will generate. Let's take the example of a smooth flat plate dragged under water. If the plate is thin and dragged along its length so it doesn't face the flow, the force measured is pretty much all due to viscous water resistance. Many countries have built special facilities, commonly known as towing tanks, to measure, among other things, the hydrodynamic forces acting on submerged bodies, dragged in water. Some of the countries discuss the data collected as part of the International Towing Tank Conference, every 3 years since 1933 (with a 9 year hiatus due to World War II). In 1957 the ITTC agreed that the formula:

was a very good approximation of the data collected. This formula is called the ITTC 1957 model-ship correlation line, and it was not deduced analytically from first principles but is rather a regression function that fits the data closely enough for practical purposes. Strictly speaking, this doesn't make much difference to us: we just need a formula of some kind that we can apply on each of our triangles to calculate viscous friction. But it does show that the physics at play in fluid dynamics is complex enough that practicians resort to measured resistance as opposed to analytical formulas.

The viscosity of the fluid is not the only parameter influencing how great the force is. For one, the roughness of the surface itself matters. A rougher surface will interact strongly with a thicker layer of water than a very smooth surface. Even more important is how turbulent the flow is around the surface. In the front of the boat, the flow is said to be laminar. It is orderly and the layers at increasing distances from the surface flow parallel to each other, albeit at different speeds since they influence each other's speed at the microscopic level due to viscosity (**). But the longer the fluid flows across a surface, the more turbulent it becomes and the more the layers start mixing with each other. When the different layers mix in a turbulent way, the amount of fluid accelerated by the surface increases and gives rise to a stronger resistance. We should therefore expect more viscous friction resistance at the back of the boat than at the front. Finally, the 3D shape of the boat matters. It differs from a flat plate which changes the nature of the flow. Since the boat is not perfectly flat, the fluid needs to travel more distance and the relative velocity of the fluid is generally greater than the velocity of the boat. Due to the shape of the boat, the pressure changes across the surface, and this also impacts resistance.

When a boat is sailing straight in calm water, the viscous resistance is the main force acting on the boat, especially. It is possible for the boat to be fairly out of the water, with very little surface opposing the motion, but with a lot of its bottom touching the water. In this case the pressure drag, which we discuss next, would be fairly small, but we would want a significant resistance from the water nevertheless. Additionally, if we were to make the boat 2 or 3 times longer without changing its facing area, we need the resistance to increase, and we get that with our viscous resistance, since it builds up mainly on the triangles of the hull tangential to the velocity.

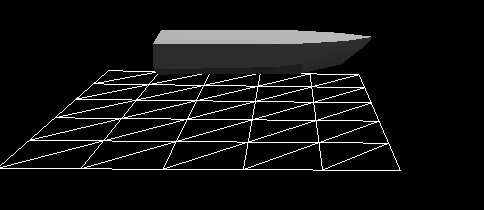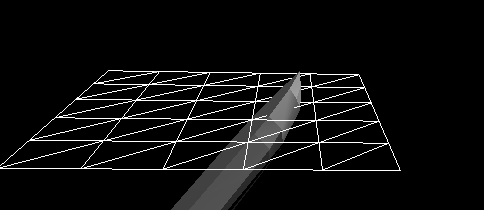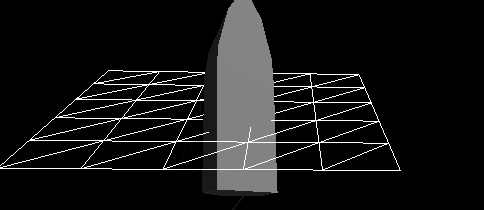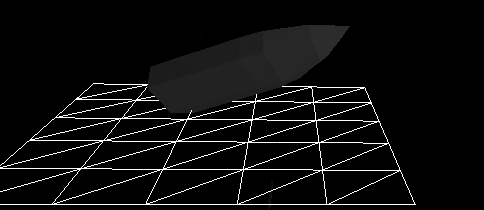
Figure 6 - Dynamic behavior of a boat subjected only to the viscous water resistance in addition to buoyancy. Even though there are very good empirical formulas for the viscous water resistance and it is fairly easy to implement, it is nowhere near enough to dampen the boat's motion. Here the boat is dropped from about a meter high above the water. The viscous water resistance plays an important role, but is only significant at higher speeds.

Pressure Drag Forces

I now turn to a second force: the pressure drag force. This is also where we depart from any serious science but I will