Last time, we created a calculator prefab with a functional display that allows us to insert expressions on it. However, we are currently unable to evaluate any of these expressions because the equal key does nothing except execute an empty method Display.Evaluate.

public void Evaluate()
{
    //TODO: implement in the second part of this tutorial
}

This is where we left off in the first part.

Today, we will be building a tokenizer, recursive descent parser, and Abstract Syntax Tree (AST), but first let's take some time to discuss some theory behind these terms to establish a solid foundation.

Tokenization, parsing, and the AST are fundamental components in the construction of a programming language. While our main focus will be creating a basic evaluator for simple mathematical expressions, if you're interested in delving deeper into this subject, I highly recommend a book called "Crafting Interpreters" by Robert Nystrom.

Tokenization, also known as lexical analysis or lexing, is the process of breaking down a sequence of characters or code into smaller units called tokens.

Let's consider an expression like (2.6+4)*8. When our tokenizer receives this string, its output will be a collection of seven tokens: (, 2.6, +, 4, ), *, and 8. Notice the tokenizer's sole responsibility is nothing more than break down the expression into these tokens, without being concerned about the validity or evaluation of the expression.

Now, let's discuss the role of a parser, a recursive descent parser to be exact. You will soon understand why it is named as such when we proceed with its implementation. For now, just note that a recursive descent parser takes in a collection of tokens and outputs an AST.

The AST is a hierarchical representation of an expression that captures the relationships between tokens. Like any tree, the AST is a graph, but note that not every graph can be considered a tree.

A graph is a data structure composed of interconnected nodes. Graphs can be classified as directed or undirected, weighted or unweighted, cyclic or acyclic and more.

Sometimes the term vertex is used instead of a node, but in this tutorial, I'm going to stick with the node.

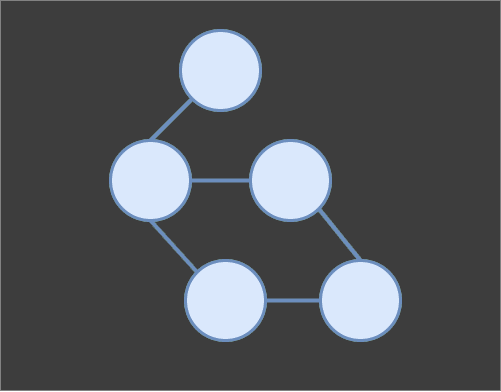An undirected graph with one cycle. 

In a tree, each node, except the root node, has a parent node and zero or more child nodes. When a node has no children, it is commonly referred to as a leaf node.

In fact, in this tutorial we're going to work with a special kind of tree, a binary tree, which is a tree where all nodes can have at most two child nodes. We can further divide binary trees to full, complete, perfect, skewed and more.

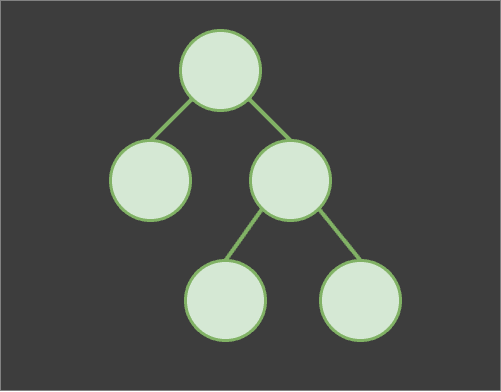A binary tree.

I won't delve into graph theory here. There are numerous resources that covers this topic much better than I would, like videos by William Fisset. This all is just a very brief overview of the absolute basics without explanations of anything that is not directly relevant to this tutorial.

I highly recommend learning more about graphs and related algorithms. Graph theory consists of one of the most, if not the most, useful concepts in computer science.

There's so much to explore for a curious mind, topics such as Depth-First Search (DFS) and Breadth-First Search (BFS), the Dijkstra, Bellman-Ford, and Floyd-Warshall algorithms, the Traveling Salesman Problem (TSP), finding cycles, bridges, and articulation points and that's only a small fraction.

While learning about graphs, you may find this library I recently wrote in C# solely for educational purposes to be useful. It implements several of the aforementioned algorithms and concepts.

Let's now get back to our parser. Once our parser completes its task of parsing the expression and constructing an AST, it returns the root node of the AST. We then invoke the Evaluate method on this root node, which recursively calls Evaluate on its child nodes. This process continues until the entire tree is evaluated.

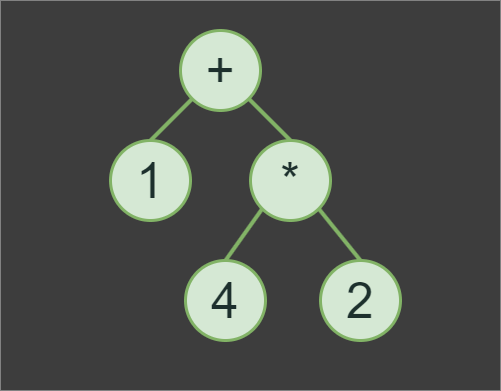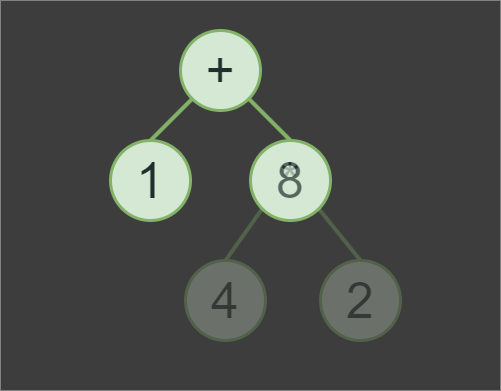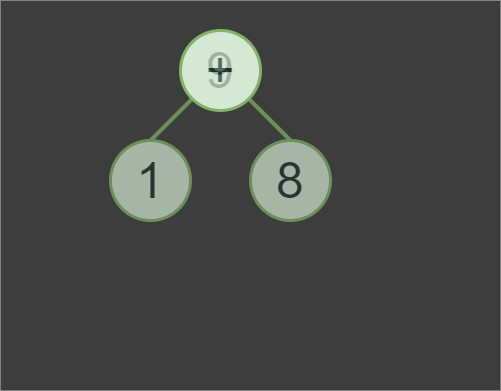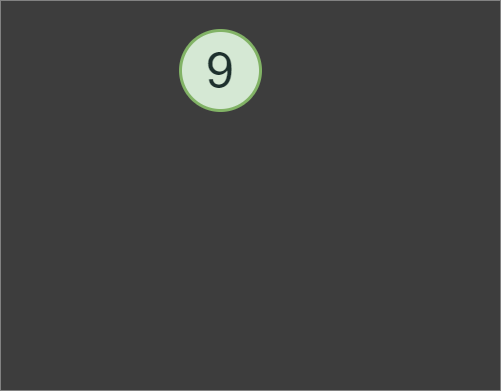AST for expression 1+4*2, we first evaluates subexpression 4*2 with the result of 8, then 8+1to produce the final result of the expression, which is 9.

In addition to implementing the Tokenizer and Parser classes, we also need to implement a Node class. However, the Node class itself will be a very minimalistic pure abstract base class for OperatorNode and OperandNode classes.

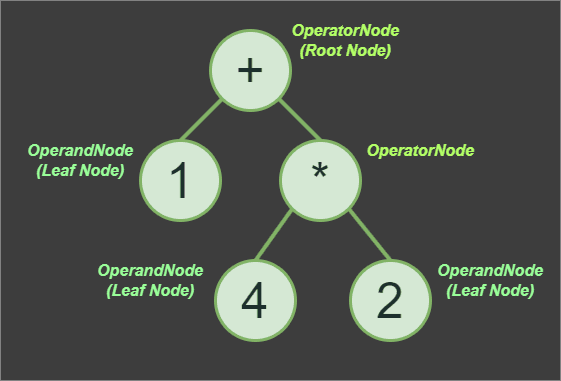The topmost node is generally called the root node, and when a node has no child nodes, we refer to it as a leaf node.

Tokenizer

Let's start by implementing a tokenizer. Create a new class in our project, name the file Tokenizer.cs, and type in the following code:

using System.Collections.Generic;
using System.Text;

public static class Tokenizer
{
    public static List<string> Tokenize(string expr)
    {
        List<string> tokens = new();
        StringBuilder buffer = new();

        foreach (char c in expr)
        {
            if (c == '+' || c == '/' || c == '*' || c == '-' || c == '(' || c == ')' || c == '^')
            {
                if (buffer.Length > 0)
                {
                    tokens.Add(buffer.ToString());
                    buffer.Clear();
                }
                tokens.Add(c.ToString());
            }
            else
            {
                buffer.Append(c);
            }
        }

        if (buffer.Length > 0)
        {
            tokens.Add(buffer.ToString());
        }

        return tokens;
    }
}

Tokenizer splits an expression into tokens.

The tokenizer starts iterating over characters in the expression If a character is one of the operators (+, -, /, *, (, ), or ^), it adds the operator to the tokens list. However, it also checks if there are any other characters in the buffer, which we utilize a StringBuilder for. If there are, a token is created in the tokens list from the buffer, and the buffer is then cleared.

If a character is not an operator, it must be either a number or a dot. The tokenizer simply appends the character to the buffer. After processing the expression, we check one last time if there are any characters in the buffer. If so, we create a final token using those characters before returning the list of tokens.

Nodes

Before we start implementing a parser, let's first implement a pure abstract Node class and its child classes, OperatorNode and OperandNode. Create a new file named Node.cs, and add in the following code:

using System;

public abstract class Node
{
    public abstract double Evaluate();
}

Node is a pure abstract class. Such a class consists solely of abstract member functions and does not include any data or concrete member functions.

Next, let's add a simple OperandNode class. In the same file, add the following code:

public class OperandNode : Node
{
    private readonly double value;

    public OperandNode(double value)
    {
        this.value = value;
    }

    public override double Evaluate()
    {
        return value;
    }
}

OperandNode class is basically a container class for a number, which in our case we internally store as a double.

The OperatorNode needs a bit more logic, yet it's still relatively small.

public class OperatorNode : Node
{
    private readonly char op;
    private readonly Node left;
    private readonly Node right;

    public OperatorNode(char op, Node left, Node right)
    {
        this.op = op;
        this.left = left;
        this.right = right;
    }

    public override double Evaluate()
    {
        return op switch
        {
            '+' => left.Evaluate() + right.Evaluate(),
            '-' => left.Evaluate() - right.Evaluate(),
            '*' => left.Evaluate() * right.Evaluate(),
            '/' => left.Evaluate() / right.Evaluate(),
            '^' => Math.Pow(left.Evaluate(), right.Evaluate()),
            _ => throw new Exception($"Unknown operator '{op}'"),
        };
    }
}

If syntax used in the Evaluate method looks new to you, this is a neat syntactic sugar that came with C# 8.0. It's called switch expression.

This is the class that allows the parser to build an AST. Notice how the OperatorNode has a members left and right, both of type Node. Each of these can be either an OperandNode, in which case the Evaluate method simply returns a value, or another OperatorNode, where the Evaluate method traverses down the tree until it reaches a leaf node.

Consider a simple expression, such as 1+2. The corresponding AST would consist of three nodes. The OperatorNode would have a member op of a value + and the OperandNodes assigned as the left and right nodes of the OperatorNode, would have values of 1 and 2, respectively.

Recursive Descent Parser

And finally, the last but also the most significant piece of the puzzle: the implementation of a parser. Let's start by adding a new file named Parser.cs. In that file, add the following code:

using System;
using System.Collections.Generic;

public class Parser
{
    private readonly List<string> tokens;
    private int pos = 0;

    public Parser(List<string> tokens)
    {
        this.tokens = tokens;
    }
}

Now, after the constructor, add a public Parse method.

public Node Parse()
{
    Node left = ParseSubAdd();
    return left;
}

Yes, you might as well just type return ParseSubAdd();

This method does nothing except calling a ParseSubAdd which we still need to implement.

private Node ParseSubAdd()
{
    Node left = ParseDivMul();
    while (pos < tokens.Count)
    {
        char op = tokens[pos++][0];
        if (op == '+' || op == '-')
        {
            Node right = ParseDivMul();
            left = new OperatorNode(op, left, right);
        }
        else
        {
             pos--;
             break;
        }
    }
    return left;
}

This method is a bit more interesting. We first call ParseDivMul, which we also need to implement, and assign the return value to a new instance of the Node class, which we named left.

Then, we start looping over tokens, and each time we increment the indexer, pos. If a token is a token for addition or subtraction, we call ParseDivMul again and we assign its result to another new instance of the Node class, this time called right.

Then, we reassign the previously created left to a new OperatorNode, where the operator is a + or - token, the left child is the previously created left node, and the right child is the newly created right node.

If the operator is neither + nor -, we decrement our indexer and break out of the loop. Then, we return the left node.

I completely understand if this is a bit confusing. It was confusing for me when I first saw it too. Bear with me, and let's implement the ParseDivMul method. After that, everything will start to become much clearer.

private Node ParseDivMul()
{
    Node left = ParseExp();
    while (pos < tokens.Count)
    {
        char op = tokens[pos++][0];
        if (op == '*' || op == '/')
        {
            Node right = ParseExp();
            left = new OperatorNode(op, left, right);
        }
        else
        {
            pos--;
            break;
        }
    }
    return left;
}

Aha! We are doing almost the exact same thing, but instead of addition and subtraction, we now care about multiplication and division and where previously we called ParseDivMul, we now calls ParseExp. Let's implement that method as well.

private Node ParseExp()
{
    Node left = ParseLeaf();
    while (pos < tokens.Count)
    {
        char op = tokens[pos++][0];
        if (op == '^')
        {
            Node right = ParseLeaf();
            left = new OperatorNode(op, left, right);
        }
        else
        {
            pos--;
            break